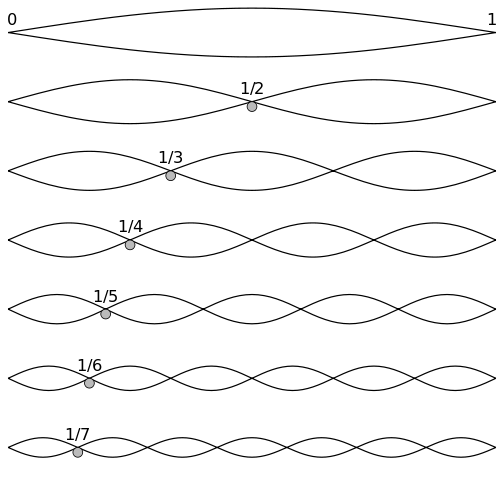
Our western scale system, based on the major scale (and relative church scales like Dorian, Mixolydian etc), seems to be following the mathematics and physics when pitching tones. With tone pitching I mean: if you take for example an A note at 440 hertz and double it you get an A at 880. This is what we call the octave. If you multiply the A440 3 times you get: 1320 hertz, this frequency (an E) is related to the A440 as a quint/fifth interval. 4 times 440 = 1760 hertz, which means it is two octaves related to the A440. If we multiply 440 with 5, we get: 2200. This tone is a C# and this is a major third interval.

You can try this yourself using a couple of strings with the same length and doing this:
– leave one like it us, untouched
– cut one string in half
– cut one string in 3 equal parts
– cut one string in 4 equal parts
– cut one string in 5 equal parts

What you just did is create the same tones as I am describing above. These strings form a major chord including 2 additional octaves. So the tonality is, thanks to the octaves, crystal clear. And it is 100% major sounding. Cool right?

But you can also use a synth. Use for example Reason’s Europa synth and select a couple of oscilators/wavetables and check your spectrum analyser:
If you set it to Basic Analog you’ll get relative pure Sine Wave tone with no overtones (only at an extremely low level, but this is how pure sine waves work: no overtones!)
If you set it to Square-Ramp you will see these overtones appear in the spectrum analyser: C3 C5 E5
If you set it to Saw-Triangle you see this: C3 C4 G4 C5 E5 G5
If you set it to Pulse Width you see this: C3 C4 G4 C5 E5 G5

So the first 5 harmonics (the 1st harmonic being the tonica, the base tone) of a NOTE are forming the notes of a major chord in the same way as we found out by multiply a note. And notice how the Square-Ramp is missing a couple of overtones, a couple of octaves. But it still creates that major third triad.

If you would look at the 7th harmonic it is a A#5. A flatted 7 . So the first harmonics are forming a major 7 chords, a blues chord, a dominant 7. Including the tritone interval. Isn’t that funky?

So the natural harmonics are simply a matter of multiplications starting from the root note.

If you have like 4 synths with a pure sine wave playing C3, C4, G4, C5, E5 & G5, this will sound the same (except for the timbre) as playing ONE note using a saw wave synth for example. The same overtones are generated.

If we take it one step further: saturation is following the exact same physics as what happens when we start cutting strings in half, 3 times etc or when we look at the natural harmonics of tones. Saturation also consists of multiplications of the root frequency in the same way, using basic calculations like 2 times, 3 times, 4 times etc.

Again these tones are forming the major scale. Multiplications of 2 and 4 will create octaves, and 3 and 5 will create an fifth and a major third. So now you will start to understand why the 1, 3 and 5 are so powerful in Western music. These tones are simply the result of simple basic physics and I am absolutely sure our brains are trained to recognise those very common intervals, simple distances between frequencies. Basic relationships our brain loves to calculate.